Qubit Cartan Decomposition¶

qitensor.experimental.cartan_decompose.unitary_from_cartan(space, alpha)¶: Returns 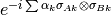$e^{-i \sum \alpha_k \sigma_{Ak} \otimes \sigma_{Bk}}$ . The space parameter should be either a bipartite qubit ket space or operator space.

qitensor.experimental.cartan_decompose.unitary_to_cartan(U)¶

Decomposes a bipartite qubit unitary into the form 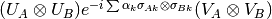$(U_A \otimes U_B) e^{-i \sum \alpha_k \sigma_{Ak} \otimes \sigma_{Bk}} (V_A \otimes V_B)$ where $\alpha_k \in (-\pi/4, \pi/4]$ . Five values are returned from this function: (UA, UB, VA, VB, alpha).

>>> from qitensor import qubit
>>> from qitensor.experimental.cartan_decompose import unitary_to_cartan
>>> from qitensor.experimental.cartan_decompose import unitary_from_cartan
>>> ha = qubit('a')
>>> hb = qubit('b')
>>> U = (ha*hb).O.random_unitary()
>>> (UA, UB, VA, VB, alpha) = unitary_to_cartan(U)
>>> Ud = unitary_from_cartan(ha*hb, alpha)
>>> # experimental module doesn't always work, so skip doctest
>>> (UA * UB * Ud * VA * VB - U).norm() < 1e-12 
True

Previous topic

Next topic

Reference (internals)

This Page