Hilbert Spaces¶

HilbertSpaces are tensor products of HilbertAtoms (although individual HilbertAtoms are also HilbertSpaces). They represent the spaces that HilbertArrays live in. A HilbertSpace is typically created by applying the multiplication operator to HilbertAtoms or other HilbertSpaces.

class qitensor.space.HilbertSpace¶

Bases: object

HilbertSpace(ket_set, bra_set, _H=None)

H¶

HilbertSpace.H(self)

The adjoint of this Hilbert space.

A HilbertSpace is returned which has bras turned into kets and kets turned into bras.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> hb = qubit('b')
>>> hc = qubit('c')
>>> sp = ha * hb * hc.H; sp
|a,b><c|
>>> sp.H
|c><a,b|
>>> sp.H.H
|a,b><c|

O¶

HilbertSpace.O(self)

The operator space for a bra or ket space.

This just returns self * self.H.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> hb = qubit('b')
>>> ha.O
|a><a|
>>> (ha*hb).O
|a,b><a,b|

P¶: P: object

addends¶: addends: object

array(self, data=None, bool noinit_data=False, bool reshape=False, input_axes=None)¶

Returns a HilbertArray created from the given data, or filled with zeros if no data is given.

If the reshape parameter is True then the given data array can be any shape as long as the total number of elements is equal to the dimension of this Hilbert space (bra dimension times ket dimension). If reshape is False (the default) then data must have an axis for each of the components of this Hilbert space.

Since it is not always clear which axes should correspond to which Hilbert space components, it is recommended when using the data parameter to also specify input_axes to tell which HilbertAtom maps to which axis of the input array. Note that there is no ambiguity if the input and output spaces are both HilbertAtoms (not composite spaces): In this case, the first axis will correspond to the ket space (if it exists) and the last axis will correspond ot the bra space (if it exists).

Parameters:

data (anything that can be used to create a numpy.array) – the array will be initialized with the data if given, otherwise it will be initialized with zeros.
noinit_data (bool; default False) – If true, the underlying numpy.array object will not be allocated. Don’t use this unless you are sure you know what you are doing.
reshape (bool; default False) – If true, the array given by the data parameter will be reshaped if needed. Otherwise, an exception will be raised if it is not the proper shape.
input_axes (tuple of HilbertAtoms) – Tells how the axes map to the space. Default is lexicographically based upon the names of the HilbertAtoms (it is not recommended to rely on this ordering).

>>> from qitensor import qubit, qudit
>>> ha = qubit('a')
>>> ha.array([1,2])
HilbertArray(|a>,
array([ 1.+0.j,  2.+0.j]))

>>> ha.H.array([1,2])
HilbertArray(<a|,
array([ 1.+0.j,  2.+0.j]))

>>> ha.O.array([[1, 2], [3, 4]])
HilbertArray(|a><a|,
array([[ 1.+0.j,  2.+0.j],
       [ 3.+0.j,  4.+0.j]]))

>>> ha.O.array([1, 2, 3, 4], reshape=True)
HilbertArray(|a><a|,
array([[ 1.+0.j,  2.+0.j],
       [ 3.+0.j,  4.+0.j]]))

>>> import numpy
>>> ha = qubit('a')
>>> hb = qudit('b', 3)
>>> hc = qudit('c', 4)
>>> arr = numpy.zeros((2, 3, 4))
>>> arr[1,0,0] = 1
>>> arr[0,1,0] = 2
>>> arr[0,0,1] = 3
>>> x = (ha*hb.H*hc).array(arr, input_axes=(ha, hb.H, hc))
>>> x.space
|a,c><b|
>>> x.nparray.shape
(2, 4, 3)
>>> x[{ ha: 1, hb.H: 0, hc: 0 }]
(1+0j)
>>> x[{ ha: 0, hb.H: 1, hc: 0 }]
(2+0j)
>>> x[{ ha: 0, hb.H: 0, hc: 1 }]
(3+0j)

assert_ket_space(self)¶

Throws an exception unless the bra space is empty.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> ha.assert_ket_space()
>>> ha.H.assert_ket_space()
Traceback (most recent call last):
    ...
NotKetSpaceError: '<a|'
>>> ha.O.assert_ket_space()
Traceback (most recent call last):
    ...
NotKetSpaceError: '|a><a|'

assert_square(self)¶

If the dimension of the bra and ket spaces are equal, returns this common dimension. Otherwise throws a HilbertShapeError.

>>> from qitensor import qudit
>>> qudit('a', 3).assert_square()
Traceback (most recent call last):
    ...
HilbertShapeError: '3 vs. 1'
>>> (qudit('a', 3) * qudit('b', 4).H).assert_square()
Traceback (most recent call last):
    ...
HilbertShapeError: '3 vs. 4'

axes¶: axes: list

axes_lookup¶: axes_lookup: dict

base_field¶: base_field: qitensor.basefield.HilbertBaseField

basis(self)¶

Returns an orthonormal basis (the computational basis) for this space.

>>> from qitensor import qubit, qudit, indexed_space
>>> import numpy
>>> ha = qubit('a')
>>> hb = qudit('b', 5)
>>> hc = indexed_space('c', ['x', 'y', 'z'])

>>> spc = ha*hb*hc.H
>>> b = spc.basis()
>>> w = [[(x.H*y).trace() for y in b] for x in b]
>>> numpy.allclose(w, numpy.eye(spc.dim()))
True

basis_vec(self, idx)¶

Returns a HilbertArray corresponding to a basis vector.

The returned vector has a 1 in the slot corresponding to idx and zeros elsewhere.

Parameters:	idx – if this Hilbert space has only one component, this should be a member of that component’s index set. Otherwise, this should be a tuple of indices.

>>> from qitensor import qubit, indexed_space
>>> ha = qubit('a')
>>> hb = qubit('b')
>>> hc = indexed_space('c', ['x', 'y', 'z'])

>>> ha.basis_vec(0)
HilbertArray(|a>,
array([ 1.+0.j,  0.+0.j]))

>>> ha.basis_vec(1)
HilbertArray(|a>,
array([ 0.+0.j,  1.+0.j]))

>>> (ha*hb).basis_vec((0, 1))
HilbertArray(|a,b>,
array([[ 0.+0.j,  1.+0.j],
       [ 0.+0.j,  0.+0.j]]))

>>> hc.basis_vec('y')
HilbertArray(|c>,
array([ 0.+0.j,  1.+0.j,  0.+0.j]))

bra_ket_set¶: bra_ket_set: frozenset

bra_set¶: bra_set: frozenset

bra_space(self) → HilbertSpace¶

Returns a HilbertSpace consisting of only the bra space of this space.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> hb = qubit('b')
>>> hc = qubit('c')
>>> sp = (ha.H * hb * hc * hc.H); sp
|b,c><a,c|
>>> sp.bra_space()
<a,c|

diag(self, v) → HilbertArray¶

Create a diagonal operator from the given 1-d list.

>>> from qitensor import qubit, qudit
>>> ha = qubit('a')
>>> hb = qudit('b', 3)

>>> ha.diag([1, 2])
HilbertArray(|a><a|,
array([[ 1.+0.j,  0.+0.j],
       [ 0.+0.j,  2.+0.j]]))
>>> ha.diag([1, 2]) == ha.H.diag([1, 2])
True
>>> ha.diag([1, 2]) == ha.O.diag([1, 2])
True

>>> op =  (ha*hb).diag([1, 2, 3, 4, 5, 6])
>>> # NOTE: spaces are ordered lexicographically
>>> op == (hb*ha).diag([1, 2, 3, 4, 5, 6])
True
>>> op.space
|a,b><a,b|
>>> import numpy
>>> numpy.diag( op.as_np_matrix() )
array([ 1.+0.j,  2.+0.j,  3.+0.j,  4.+0.j,  5.+0.j,  6.+0.j])

dim(self) → int¶

Returns the dimension of this space.

>>> from qitensor import qubit, qudit, indexed_space
>>> ha = qubit('a')
>>> hb = qudit('b', 5)
>>> hc = indexed_space('c', ['x', 'y', 'z'])

>>> ha.dim()
2
>>> (ha*hb*hc.H).dim()
30

empty_space(self)¶

Returns a TensorSubspace corresponding to the empty space.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> ha.empty_space()
<TensorSubspace of dim 0 over space (|a>)>
>>> ha.O.empty_space()
<TensorSubspace of dim 0 over space (|a><a|)>

eye(self) → HilbertArray¶

Returns a HilbertArray corresponding to the identity matrix.

If the bra space or ket space is empty, then the nonempty of those two is used to form an operator space (i.e. self.O). If both the bra and ket spaces are nonempty, they must be of the same dimension since the identity matrix must be square.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> hb = qubit('b')

>>> ha.eye()
HilbertArray(|a><a|,
array([[ 1.+0.j,  0.+0.j],
       [ 0.+0.j,  1.+0.j]]))

>>> (ha*hb.H).eye()
HilbertArray(|a><b|,
array([[ 1.+0.j,  0.+0.j],
       [ 0.+0.j,  1.+0.j]]))

>>> ha.eye() == ha.H.eye()
True
>>> ha.eye() == ha.O.eye()
True

fourier(self) → HilbertArray¶

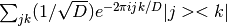
Returns the Fourier transform gate. The returned operator is $\sum_{jk} (1/\sqrt{D}) e^{-2 \pi i j k/D} |j><k|$

If the bra space or ket space is empty, then the nonempty of those two is used to form an operator space (i.e. self.O). If both the bra and ket spaces are nonempty, they must be of the same dimension since the operator must be square.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> hb = qubit('b')

>>> ha.fourier()
HilbertArray(|a><a|,
array([[ 0.707107+0.j,  0.707107+0.j],
       [ 0.707107+0.j, -0.707107-0.j]]))

>>> (ha*hb.H).fourier()
HilbertArray(|a><b|,
array([[ 0.707107+0.j,  0.707107+0.j],
       [ 0.707107+0.j, -0.707107-0.j]]))

>>> (ha*hb).fourier()
HilbertArray(|a,b><a,b|,
array([[[[ 0.5+0.j ,  0.5+0.j ],
         [ 0.5+0.j ,  0.5+0.j ]],

        [[ 0.5+0.j ,  0.0-0.5j],
         [-0.5-0.j , -0.0+0.5j]]],


       [[[ 0.5+0.j , -0.5-0.j ],
         [ 0.5+0.j , -0.5-0.j ]],

        [[ 0.5+0.j , -0.0+0.5j],
         [-0.5-0.j ,  0.0-0.5j]]]]))

fourier_basis_state(self, int k) → HilbertArray¶

Returns a state from the Fourier basis.

The returned state is 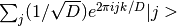$\sum_j (1/\sqrt{D}) e^{2 \pi i j k/D} |j>$ where D is the dimension of the space and j is an integer (regardless of the actual values of the index set).

>>> from qitensor import qubit, qudit, indexed_space

>>> ha = qudit('a', 4)
>>> ha.fourier_basis_state(0)
HilbertArray(|a>,
array([ 0.5+0.j,  0.5+0.j,  0.5+0.j,  0.5+0.j]))
>>> ha.fourier_basis_state(1)
HilbertArray(|a>,
array([ 0.5+0.j ,  0.0+0.5j, -0.5+0.j , -0.0-0.5j]))
>>> hb = qubit('b')
>>> (ha*hb).fourier_basis_state(0)
HilbertArray(|a,b>,
array([[ 0.353553+0.j,  0.353553+0.j],
       [ 0.353553+0.j,  0.353553+0.j],
       [ 0.353553+0.j,  0.353553+0.j],
       [ 0.353553+0.j,  0.353553+0.j]]))
>>> (ha*hb).fourier_basis_state(3) == (ha*hb).H.fourier_basis_state(3).H
True
>>> (ha*hb.H).fourier_basis_state(0)
Traceback (most recent call last):
    ...
HilbertError: 'fourier_basis_state not allowed for operators (only for bras or kets)'
>>> hc = indexed_space('c', ['w', 'x', 'y', 'z'])
>>> hc.fourier_basis_state(0)
HilbertArray(|c>,
array([ 0.5+0.j,  0.5+0.j,  0.5+0.j,  0.5+0.j]))

full_space(self)¶

Returns a TensorSubspace corresponding to the entire space.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> ha.full_space()
<TensorSubspace of dim 2 over space (|a>)>
>>> ha.O.full_space()
<TensorSubspace of dim 4 over space (|a><a|)>

fully_mixed(self) → HilbertArray¶

Returns the fully mixed state.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> hb = qubit('b')

>>> ha.fully_mixed()
HilbertArray(|a><a|,
array([[ 0.5+0.j,  0.0+0.j],
       [ 0.0+0.j,  0.5+0.j]]))

>>> ha.fully_mixed() == ha.H.fully_mixed()
True
>>> ha.fully_mixed() == ha.O.fully_mixed()
True

haar_matrix(self) → HilbertArray¶

Returns the unitary matrix for the Haar wavelet transform. Only applies if the dimension of the space is a power of 2.

>>> from qitensor import qudit

>>> ha = qudit('a', 1)
>>> ha.haar_matrix()
HilbertArray(|a><a|,
array([[ 1.+0.j]]))

>>> ha = qudit('a', 2)
>>> ha.haar_matrix()
HilbertArray(|a><a|,
array([[ 0.707107+0.j,  0.707107+0.j],
       [ 0.707107+0.j, -0.707107+0.j]]))

>>> ha = qudit('a', 4)
>>> ha.haar_matrix()
HilbertArray(|a><a|,
array([[ 0.500000+0.j,  0.500000+0.j,  0.500000+0.j,  0.500000+0.j],
       [ 0.500000+0.j,  0.500000+0.j, -0.500000+0.j, -0.500000+0.j],
       [ 0.707107+0.j, -0.707107+0.j,  0.000000+0.j,  0.000000+0.j],
       [ 0.000000+0.j,  0.000000+0.j,  0.707107+0.j, -0.707107+0.j]]))

>>> ha.haar_matrix() == ha.O.haar_matrix()
True

hadamard(self) → HilbertArray¶

Returns the Hadamard matrix. Only applies if the dimension of the space is a power of 2. The returned operator is 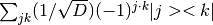$\sum_{jk} (1/\sqrt{D}) (-1)^{j \cdot k} |j><k|$ where j, k are bitstrings.

>>> from qitensor import qubit, qudit
>>> import numpy as np
>>> import numpy.linalg as linalg

>>> ha = qubit('a')
>>> ha.hadamard()
HilbertArray(|a><a|,
array([[ 0.707107+0.j,  0.707107+0.j],
       [ 0.707107+0.j, -0.707107+0.j]]))
>>> ha.hadamard() == ha.O.hadamard()
True

>>> hb = [qubit('b%d' % i) for i in range(5)]
>>> U = np.product([ h.hadamard() for h in hb ])
>>> hc = qudit('c', 2**5)
>>> V = hc.hadamard()
>>> linalg.norm( U.as_np_matrix() - V.as_np_matrix() ) < 1e-14
True

hermitian_basis(self, normalize=False, tracefree=False)¶

Returns an orthogonal basis (optionally normalized) of Hermitian operators. It is required that the dimension of the bra space be equal to that of the ket space. Real linear combinations of these basis operators will be Hermitian. If the tracefree option is specified then the returned basis only covers the 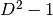$D^2-1$ dimensional subspace.

>>> from qitensor import qubit, qudit, indexed_space
>>> import numpy
>>> import numpy.random

>>> ha = qudit('a', 7)
>>> spc = ha.O

>>> b = spc.hermitian_basis(normalize=True)
>>> len(b) == ha.dim() ** 2
True
>>> numpy.allclose([[(x.H*y).trace() for y in b] for x in b], numpy.eye(spc.dim()))
True
>>> numpy.all([(x-x.H).norm() < 1e-12 for x in b])
True
>>> y = numpy.sum([x * numpy.random.rand() for x in b])
>>> (y - y.H).norm() < 1e-12
True

>>> tf = spc.hermitian_basis(normalize=True, tracefree=True)
>>> len(tf) == ha.dim() ** 2 - 1
True
>>> numpy.allclose([[(x.H*y).trace() for y in tf] for x in tf], numpy.eye(spc.dim()-1))
True
>>> numpy.all([(x-x.H).norm() < 1e-12 for x in tf])
True
>>> y = numpy.sum([x * numpy.random.rand() for x in tf])
>>> (y - y.H).norm() < 1e-12
True

>>> hb = indexed_space('b', ['x', 'y', 'z'])
>>> hc = qudit('c', 3)
>>> spc = hb * hc.H
>>> b = spc.hermitian_basis(normalize=True)
>>> numpy.allclose([[(x.H*y).trace() for y in b] for x in b], numpy.eye(spc.dim()))
True

index_iter(self)¶

Returns an iterator over the indices of this space. Each returned value is a tuple.

See also: indices(), index_iter_dict()

>>> from qitensor import qubit, qudit, indexed_space
>>> ha = qubit('a')
>>> hb = qudit('b', 5)
>>> hc = indexed_space('c', ['x', 'y', 'z'])

>>> list(ha.index_iter())
[(0,), (1,)]

>>> list((ha*hc).index_iter())
[(0, 'x'), (0, 'y'), (0, 'z'), (1, 'x'), (1, 'y'), (1, 'z')]

>>> len(list( (ha*hb*hc).index_iter() )) == (ha*hb*hc).dim()
True

>>> x = (ha * hb * hc.H).random_array()
>>> norm2 = sum(abs(x[idx])**2 for idx in x.space.index_iter())
>>> abs(norm2 - x.norm()**2) < 1e-12
True

index_iter_dict(self)¶

Returns an iterator over the indices of a space. Each returned value is a dictionary.

See also: indices(), index_iter()

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> hb = qubit('b')

>>> list((ha*hb.H).index_iter_dict()) == [{ha: 0, hb.H: 0}, {ha: 0, hb.H: 1}, {ha: 1, hb.H: 0}, {ha: 1, hb.H: 1}]
True

>>> x = (ha*hb.H).random_unitary()
>>> x.space
|a><b|
>>> [ x[idx].space for idx in ha.index_iter_dict() ]
[<b|, <b|]
>>> [ "%.3f" % x[idx].norm() for idx in ha.index_iter_dict() ]
['1.000', '1.000']

is_square(self)¶

If the dimension of the bra and ket spaces are equal, returns this common dimension. Otherwise returns zero.

>>> from qitensor import qubit, qudit
>>> ha = qubit('a')
>>> hb = qudit('b', 3)
>>> ha.is_square()
0
>>> ha.O.is_square()
2
>>> (ha*hb.H).is_square()
0
>>> (ha*hb).O.is_square()
6

is_symmetric(self)¶: Check whether the bra and ket spaces are the same. >>> from qitensor import qubit >>> ha = qubit(‘a’) >>> hb = qubit(‘b’) >>> ha.is_symmetric() False >>> ha.O.is_symmetric() True >>> (ha * hb.H).is_symmetric() False >>> (ha * hb.H * ha.H * hb).is_symmetric() True

ket_set¶: ket_set: frozenset

ket_space(self) → HilbertSpace¶

Returns a HilbertSpace consisting of only the ket space of this space.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> hb = qubit('b')
>>> hc = qubit('c')
>>> sp = (ha.H * hb * hc * hc.H); sp
|b,c><a,c|
>>> sp.ket_space()
|b,c>

prime¶

HilbertSpace.prime(self)

Returns a HilbertSpace just like this one but with an apostrophe appended to each label.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> hb = qubit('b')
>>> (ha*hb).prime
|a',b'>
>>> (ha*hb).prime.prime
|a'',b''>
>>> ha.O.prime
|a'><a'|

random_array(self) → HilbertArray¶

Returns a HilbertArray with random values.

The values are complex numbers drawn from a standard normal distribution.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> ha.random_array() 
HilbertArray(|a>,
array([-0.484410+0.426767j,  0.000693+0.912554j]))

random_density(self) → HilbertArray¶

Returns a random density matrix.

>>> from qitensor import qubit, qudit

>>> ha = qubit('a')
>>> hb = qudit('b', 3)
>>> ha.random_density().space
|a><a|
>>> ha.H.random_density().space
|a><a|
>>> ha.O.random_density().space
|a><a|
>>> (ha*hb).random_density().space
|a,b><a,b|
>>> (ha*hb.H).random_density()
Traceback (most recent call last):
    ...
HilbertError: 'not a symmetric operator space: |a><b|'
>>> tr = (ha*hb).random_density().trace()
>>> np.abs(tr - 1) < 1e-14
True

random_isometry(self) → HilbertArray¶

Returns a random isometry.

The ket space must be at least as great in dimension as the bra space.

>>> from qitensor import qubit, qudit

>>> ha = qubit('a')
>>> hb = qudit('b', 7)
>>> hc = qudit('c', 3)
>>> m = (ha * hb * hc.H).random_isometry()
>>> (m.H * m - hc.eye()).norm() < 1e-14
True
>>> m = (hb * ha.H * hc.H).random_isometry()
>>> (m.H * m - (ha*hc).eye()).norm() < 1e-14
True

random_unitary(self) → HilbertArray¶

Returns a random unitary.

If the bra space or ket space is empty, then the nonempty of those two is used to form an operator space (i.e. self.O). If both the bra and ket spaces are nonempty, they must be of the same dimension since a unitary matrix must be square.

The returned unitary is drawn from a distribution uniform with respect to the Haar measure, using the algorithm by Mezzadri, “How to Generate Random Matrices from the Classical Compact Groups”, Notices of the AMS 54, 592 (2007).

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> hb = qubit('b')
>>> m = ha.random_unitary()
>>> (m.H * m - ha.eye()).norm() < 1e-14
True
>>> (m * m.H - ha.eye()).norm() < 1e-14
True
>>> (ha.random_unitary() - ha.random_unitary()).norm() < 1e-14
False
>>> m = (ha.H * hb).random_unitary()
>>> m.space
|b><a|
>>> (m.H * m - ha.eye()).norm() < 1e-14
True
>>> (m * m.H - hb.eye()).norm() < 1e-14
True

reshaped_np_matrix(self, m, input_axes=None)¶

Returns a HilbertArray created from a given numpy matrix.

The number of rows and columns must match the dimensions of the ket and bra spaces. It is required that len(m.shape)==2. The input_axes parameter gives the storage order of the input data, and is recommended when the input spaces are composites (not HilbertAtoms).

Parameters:	m (numpy.matrix or numpy.array) – the input matrix. input_axes (list) – the storage order for the input data

Hilbert Spaces¶

Previous topic

Next topic

This Page

Navigation

Hilbert Spaces¶

Previous topic

Next topic

This Page

Quick search

Navigation