Arrays (a.k.a. vectors, tensors, operators)¶
A HilbertArray is a vector in a HilbertSpace. Internally, it is backed by a numpy.array. HilbertArray’s are to be created using the HilbertSpace.array() method.
- class qitensor.array.HilbertArray¶
Bases: object
HilbertArray(HilbertSpace space, data, bool noinit_data, bool reshape, input_axes)
- H¶
HilbertArray.H(self)
Returns the adjoint (Hermitian conjugate) of this array.
>>> from qitensor import qubit >>> ha = qubit('a') >>> x = ha.array([1j, 0]); x HilbertArray(|a>, array([ 0.+1.j, 0.+0.j])) >>> x.H HilbertArray(<a|, array([ 0.-1.j, 0.-0.j])) >>> y = ha.O.array([[1+2j, 3+4j], [5+6j, 7+8j]]); y HilbertArray(|a><a|, array([[ 1.+2.j, 3.+4.j], [ 5.+6.j, 7.+8.j]])) >>> y.H HilbertArray(|a><a|, array([[ 1.-2.j, 5.-6.j], [ 3.-4.j, 7.-8.j]]))
- I¶
HilbertArray.I(self)
Returns the matrix inverse of this array.
It is required that the dimension of the bra space be equal to the dimension of the ket space.
This is just a shortcut for self.inv(), which offers more options.
See also: inv()
>>> from qitensor import qubit, qudit >>> ha = qubit('a') >>> x = ha.O.random_array() >>> (x * x.I - ha.eye()).norm() < 1e-13 True >>> hb = qubit('b') >>> hc = qudit('c', 4) >>> y = (ha * hb * hc.H).random_array() >>> (y * y.I - (ha * hb).eye()).norm() < 1e-13 True >>> (y.I * y - hc.eye()).norm() < 1e-13 True
- O¶
HilbertArray.O(self)
Makes a density operator from a pure state.
The input must be a ket vector. The output is self * self.H.
>>> from qitensor import qubit >>> ha = qubit('a') >>> x = ha.array([1j, 2]); x HilbertArray(|a>, array([ 0.+1.j, 2.+0.j])) >>> x.O HilbertArray(|a><a|, array([[ 1.+0.j, 0.+2.j], [ 0.-2.j, 4.+0.j]]))
- QR(self, inner_space=None)¶
Returns operators Q and R such that Q is an isometry, R is upper triangular, and self=Q*R.
The bra space of Q (and the ket space of R) is the smaller of the bra or ket spaces of the input. This can be overridden using the inner_space parameter.
Parameters: inner_space (HilbertSpace) – bra space of Q (and the ket space of R) >>> from qitensor import qubit >>> ha = qubit('a') >>> hb = qubit('b') >>> hc = qubit('c') >>> m = (hb*hc*ha.H).random_array() >>> (q, r) = m.QR() >>> (q.space, r.space) (|b,c><a|, |a><a|) >>> (q.H * q - ha.eye()).norm() < 1e-14 True >>> (q*r - m).norm() < 1e-14 True >>> (q, r) = ha.O.random_array().QR(inner_space=hb) >>> (q.space, r.space) (|a><b|, |b><a|)
- T¶
HilbertArray.T(self)
Returns the transpose of this array.
>>> from qitensor import qubit >>> ha = qubit('a') >>> x = ha.array([1j, 0]); x HilbertArray(|a>, array([ 0.+1.j, 0.+0.j])) >>> x.T HilbertArray(<a|, array([ 0.+1.j, 0.+0.j])) >>> y = ha.O.array([[1+2j, 3+4j], [5+6j, 7+8j]]); y HilbertArray(|a><a|, array([[ 1.+2.j, 3.+4.j], [ 5.+6.j, 7.+8.j]])) >>> y.T HilbertArray(|a><a|, array([[ 1.+2.j, 5.+6.j], [ 3.+4.j, 7.+8.j]]))
- apply_map(self, fn)¶
Apply the given function to each element of the array.
>>> from qitensor import qubit >>> ha = qubit('a') >>> v = ha.array([1, -2]) >>> v.apply_map(lambda x: abs(x)) HilbertArray(|a>, array([ 1.+0.j, 2.+0.j]))
- as_np_matrix(self, dtype=None, row_space=None, col_space=None)¶
Returns the underlying data as a numpy.matrix. Returns a copy, not a view.
Parameters: - dtype – datatype of returned matrix.
- row_space (HilbertSpace, list, or tuple) – the HilbertSpace to use for the row space of the matrix, default is the bra space of the input array.
- col_space (HilbertSpace, list, or tuple) – the HilbertSpace to use for the column space of the matrix, default is the ket space of the input array.
>>> import numpy >>> from qitensor import qubit, qudit >>> ha = qubit('a') >>> hb = qudit('b', 3) >>> x = (ha.O * hb).random_array() >>> x.space |a,b><a| >>> x.as_np_matrix().shape (6, 2) >>> # returns a copy, not a view >>> x.as_np_matrix().fill(0); x.norm() == 0 False >>> x.as_np_matrix(col_space=ha.O).shape (4, 3) >>> x.as_np_matrix(row_space=ha.O).shape (3, 4) >>> numpy.allclose(x.as_np_matrix(col_space=ha.O), x.as_np_matrix(row_space=ha.O).T) True
- assert_density_matrix(self, check_hermitian=True, check_normalized=True, check_positive=True)¶
Throws an error unless the input is a density matrix.
>>> from qitensor import qubit >>> ha = qubit('a') >>> hb = qubit('b')
>>> ha.random_density().assert_density_matrix() >>> # small errors are accepted >>> (ha.random_density() + ha.O.random_array()*1e-14).assert_density_matrix()
>>> ha.eye().assert_density_matrix() Traceback (most recent call last): ... HilbertError: 'density matrix was not normalized: trace=(2+0j)'
>>> (ha.ket(0) * hb.bra(0)).assert_density_matrix() Traceback (most recent call last): ... HilbertError: 'not a density matrix: |a><b|'
>>> ha.random_unitary().assert_density_matrix() Traceback (most recent call last): ... HilbertError: 'not a density matrix: not Hermitian'
>>> U = ha.random_unitary() >>> (U * ha.diag([ 1.1, -0.1 ]) * U.H).assert_density_matrix() Traceback (most recent call last): ... HilbertError: 'not a density matrix: had negative eigenvalue (-0.1)'
- axes¶
axes: list
- closeto(self, other, rtol=1e-05, atol=1e-08)¶
Checks whether two arrays are nearly equal, similar to numpy.allclose.
For details, see the numpy.allclose documentation.
>>> from qitensor import qudit >>> ha = qudit('a', 10) >>> x = ha.random_array() >>> y = ha.random_array() >>> x.closeto(y) False >>> x.closeto(x * (1+1e-10)) True >>> x == x * (1+1e-10) False
- conj(self)¶
Returns the complex conjugate of this array.
>>> from qitensor import qubit >>> ha = qubit('a') >>> x = ha.array([1j, 0]); x HilbertArray(|a>, array([ 0.+1.j, 0.+0.j])) >>> x.conj() HilbertArray(|a>, array([ 0.-1.j, 0.-0.j])) >>> y = ha.O.array([[1+2j, 3+4j], [5+6j, 7+8j]]); y HilbertArray(|a><a|, array([[ 1.+2.j, 3.+4.j], [ 5.+6.j, 7.+8.j]])) >>> y.conj() HilbertArray(|a><a|, array([[ 1.-2.j, 3.-4.j], [ 5.-6.j, 7.-8.j]]))
- conj_by(self, U)¶
Returns U*self*U.H.
>>> from qitensor import qubit >>> ha = qubit('a') >>> U = ha.random_unitary() >>> x = ha.random_density() >>> (U*x*U.H - x.conj_by(U)).norm() < 1e-13 True
- copy(self)¶
Creates a copy (not a view) of this array.
>>> from qitensor import qubit >>> ha = qubit('a') >>> x = ha.array([1, 2]); x HilbertArray(|a>, array([ 1.+0.j, 2.+0.j])) >>> y = x.copy() >>> y[0] = 3 >>> y HilbertArray(|a>, array([ 3.+0.j, 2.+0.j])) >>> x HilbertArray(|a>, array([ 1.+0.j, 2.+0.j]))
- det(self)¶
Returns the matrix determinant of this array.
It is required that the dimension of the bra space be equal to the dimension of the ket space.
>>> import numpy.linalg >>> from qitensor import qubit, qudit >>> ha = qubit('a') >>> hb = qubit('b') >>> hc = qudit('c', 4) >>> y = (ha * hb * hc.H).random_array() >>> abs( y.det() - numpy.linalg.det(y.as_np_matrix()) ) < 1e-14 True
- diag(self, as_np=False)¶
Returns the diagonal elements of this operator, as a ket vector (if as_np=False) or as a numpy array (if as_np=True). Only applicable to square operators.
>>> from qitensor import qubit >>> ha = qubit('a') >>> hb = qubit('b') >>> A = ha.O.array([[1,2],[3,4]]) >>> B = hb.O.array([[1,10],[100,1000]]) >>> A.diag() HilbertArray(|a>, array([ 1.+0.j, 4.+0.j])) >>> A.diag(as_np=True) array([ 1.+0.j, 4.+0.j]) >>> (A*B).diag() HilbertArray(|a,b>, array([[ 1.+0.j, 1000.+0.j], [ 4.+0.j, 4000.+0.j]])) >>> (A*B).diag(as_np=True) array([ 1.+0.j, 1000.+0.j, 4.+0.j, 4000.+0.j])
- eig(self, w_space=None, hermit=False)¶
Return the eigenvalues and right eigenvectors of this array.
Parameters: - w_space (HilbertSpace; default None) – space for the diagonal matrix, if None the space of the input array is used.
- hermit (bool; default False) – set this to True if the input is Hermitian
NOTE: in the case of degenerate eigenvalues, with hermit=False, it may be the case that the returned eigenvectors array is not full rank. See the documentation for numpy.linalg.eig for details.
>>> from qitensor import qubit, qudit >>> ha = qubit('a') >>> hb = qudit('b', 3) >>> hc = qudit('c', 6) >>> epsilon = 1e-13
>>> op = (ha*hb).O.random_array() >>> # make a normal operator >>> op = op.H * op >>> (W, V) = op.eig() >>> V.space |a,b><a,b| >>> W.space |a,b><a,b| >>> (V.H * V - (ha*hb).eye()).norm() < epsilon True >>> (V.H * op * V - W).norm() < epsilon True >>> (op * V - V * W).norm() < epsilon True
>>> # NOTE: this is not a normal operator, so V won't be unitary. >>> op = (ha*hb).O.random_array() >>> (W, V) = op.eig(w_space=hc) >>> V.space |a,b><c| >>> W.space |c><c| >>> (op * V - V * W).norm() < epsilon True
>>> vec = hb.random_array().normalized() >>> dyad = vec * vec.H >>> (W, V) = dyad.eig(hermit=True) >>> (W - hb.diag([1, 0, 0])).norm() < epsilon True >>> (V.H * V - hb.eye()).norm() < epsilon True >>> vec2 = V[:, 0] >>> # Correct for phase ambiguity >>> vec2 *= (vec[0]/vec2[0]) / abs(vec[0]/vec2[0]) >>> (vec - vec2).norm() < epsilon True
- eigvals(self, hermit=False)¶
Return the eigenvalues of this array, sorted in order of decreasing real component.
Parameters: hermit (bool; default False) – set this to True if the input is Hermitian. In this case, the returned eigenvalues will be real. >>> from qitensor import qubit, qudit >>> ha = qubit('a') >>> hb = qudit('b', 3) >>> epsilon = 1e-13
>>> op = (ha*hb).O.random_array() >>> # make a normal operator >>> op = op.H * op >>> (W1, V1) = op.eig() >>> W2 = op.eigvals() >>> (ha*hb).diag(W2) == W1 True
- entropy(self, normalize=False, checks=True)¶
Returns the von Neumann entropy of a density operator, in bits.
Parameters: - normalize (bool; default False) – if True, the input is automatically normalized to trace one. If false, an exception is raised if the trace is not one.
- checks (bool; default True) – if False, don’t check that the input is a valid density matrix or Hermitian. This is sometimes needed for symbolic computations.
>>> import numpy as np >>> from qitensor import qubit, qudit >>> ha = qubit('a') >>> hb = qudit('b', 3) >>> # entropy of a pure state is zero >>> ha.ket(0).O.entropy() 0.0 >>> # a fully mixed state of dimension 2 >>> (ha.ket(0).O/2 + ha.ket(1).O/2).entropy() 1.0 >>> # a fully mixed state of dimension 3 >>> abs( (hb.eye()/3).entropy() - np.log2(3) ) < 1e-10 True >>> # automatic normalization >>> abs( hb.eye().entropy(normalize=True) - np.log2(3) ) < 1e-10 True >>> # a bipartite pure state >>> s = (ha.ket(0) * hb.array([1/np.sqrt(2),0,0]) + ha.ket(1) * hb.array([0,0.5,0.5])) >>> np.round(s.O.entropy(), 10) 0.0 >>> # entanglement across the a-b cut >>> (s.O.trace(hb)).entropy() 1.0 >>> # entanglement across the a-b cut is the same as across b-a cut >>> s = (ha*hb).random_array().normalized().O >>> abs(s.trace(ha).entropy() - s.trace(hb).entropy()) < 1e-10 True
- expm(self)¶
Return the matrix exponential of this array.
It is required that the dimension of the bra space be equal to the dimension of the ket space.
>>> import numpy >>> from qitensor import qubit >>> ha = qubit('a') >>> ((ha.X * numpy.pi * 1j).expm() + ha.eye()).norm() < 1e-12 True
- fill(self, val)¶
Fills every entry of this array with a constant value.
NOTE: the array is modified in-place and is not returned.
>>> from qitensor import qubit >>> ha = qubit('a') >>> x = ha.random_array() >>> x.fill(2) >>> x HilbertArray(|a>, array([ 2.+0.j, 2.+0.j]))
- get_dim(self, atom)¶
Returns the axis corresponding to the given HilbertAtom.
This is useful when working with the underlying numpy array.
>>> from qitensor import qubit >>> ha = qubit('a') >>> hb = qubit('b') >>> x = (ha * hb).array([[1, 2], [4, 8]]) >>> [x.get_dim(h) for h in (ha, hb)] [0, 1] >>> x.nparray.sum(axis=x.get_dim(ha)) array([ 5.+0.j, 10.+0.j]) >>> x.nparray.sum(axis=x.get_dim(hb)) array([ 3.+0.j, 12.+0.j])
- inv(self, row_space=None)¶
Returns the matrix inverse of this array.
Parameters: row_space (HilbertSpace, list, or tuple) – the HilbertSpace to use for the row space of the matrix, default is the bra space of the input array. This parameter allows computing the inverse of the cross operator. See also: I()
>>> from qitensor import qubit, qudit >>> import numpy.linalg >>> ha = qubit('a') >>> hb = qubit('b') >>> hc = qudit('c', 4)
>>> x = ha.O.random_array() >>> (x * x.inv() - ha.eye()).norm() < 1e-13 True
>>> y = (ha * hb * hc.H).random_array() >>> (y.space, y.inv().space) (|a,b><c|, |c><a,b|) >>> (y * y.inv() - (ha * hb).eye()).norm() < 1e-13 True >>> (y.inv() * y - hc.eye()).norm() < 1e-13 True
>>> z = (ha * hc * hb.H).random_array() >>> (z.space, z.inv(hc).space) (|a,c><b|, |b><a,c|) >>> ((z * z.inv(hc)).trace(ha) - hc.eye()).norm() < 1e-14 True >>> (z.inv(hc).tensordot(z, contraction_spaces=hc) - (ha*hb).O.eye()).norm() < 1e-14 True
- lmul(self, other)¶
Returns other*self.
This is useful for listing operations in chronoligical order when implementing quantum circuits.
>>> from qitensor import qubit >>> ha = qubit('a') >>> state = ha.random_array() >>> ha.X * ha.Y * state == state.lmul(ha.Y).lmul(ha.X) True
- logm(self)¶
Return the matrix logarithm of this array.
It is required that the dimension of the bra space be equal to the dimension of the ket space.
>>> from qitensor import qubit >>> ha = qubit('a') >>> hb = qubit('b') >>> op = ha.X * hb.Z >>> (op.logm().expm() - op).norm() < 1e-14 True
- measure(self, HilbertSpace spc=None, bool normalize=False) → tuple¶
Performs a measurement of a quantum state (ket or density operator) in the computational basis.
The result is random, with probability distribution consistent with the laws of quantum mechanics. The return value is a tuple, with the first element being the index corresponding to the measurement outcome and the second element being the density operator corresponding to the state of the remaining subsystems (or the value 1 if there are none).
FIXME - this function is under development and the usage will change. For example, for a ket input, the “remaining subsystems” state should be returned as a ket rather than a density operator.
FIXME - doctests #>>> from qitensor import qudit #>>> ha=qudit(‘a’, 3); hb=qudit(‘b’, 4); x = (ha*hb).random_array() #>>> x.measure()
- mutual_info(self, ha, hb)¶
FIXME - docs
- n(self, prec=None, digits=None)¶
Converts symbolic values to numeric values (only useful in Sage).
sage: from qitensor import qubit sage: ha = qubit(‘a’, dtype=SR) sage: v = ha.array([log(4), log(8)])
sage: v HilbertArray(|a>, array([log(4), log(8)], dtype=object))
sage: v.n() HilbertArray(|a>, array([1.38629436111989, 2.07944154167984], dtype=object))
- norm(self, p=2)¶
Returns the vector norm of this array. If p is given, then the
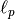 norm is computed.
norm is computed.See also: schatten_norm(), trace_norm()
>>> from qitensor import qubit, qudit >>> ha = qubit('a') >>> x = ha.array([3, 4]) >>> x.norm() 5.0 >>> y = ha.O.array([[1, 2], [3, 4]]) >>> y.norm() ** 2 30.0 >>> y.norm(p=1) 10.0 >>> y.norm(p=np.inf) 4.0 >>> hb = qudit('b', 6) >>> x = hb.array([1, 1, 1, 2, 2, 2]) >>> x.norm(3) 3.0
- normalize(self)¶
Normalizes array in-place.
See also: normalized()
>>> from qitensor import qubit >>> ha = qubit('a') >>> x = ha.array([3, 4]) >>> x.normalize() >>> x HilbertArray(|a>, array([ 0.6+0.j, 0.8+0.j]))
- normalized(self)¶
Returns a normalized copy of this array.
See also: normalize()
>>> from qitensor import qubit >>> ha = qubit('a') >>> x = ha.array([3, 4]) >>> x.normalized() HilbertArray(|a>, array([ 0.6+0.j, 0.8+0.j]))
- np_matrix_transform(self, f, transpose_dims=False, row_space=None, col_space=None)¶
Performs a numpy matrix operation.
Parameters: - f (lambda function) – operation to perform
- transpose_dims (bool) – if True, the resultant Hilbert space is transposed
- row_space (HilbertSpace, list, or tuple) – the HilbertSpace to use for the row space of the matrix, default is the bra space of the input array.
- col_space (HilbertSpace, list, or tuple) – the HilbertSpace to use for the column space of the matrix, default is the ket space of the input array.
>>> from qitensor import qubit, qudit >>> import numpy.linalg >>> ha = qubit('a') >>> hb = qubit('b') >>> hc = qudit('c', 4)
>>> x = (ha * hb.H).random_array() >>> x.space |a><b| >>> y = x.np_matrix_transform(numpy.linalg.inv, transpose_dims=True) >>> y.space |b><a| >>> y == x.I True
>>> v = ha.random_array() >>> (v.np_matrix_transform(lambda x: x*2) - v*2).norm() < 1e-14 True
>>> w = (ha*hc*hb.H).random_array() >>> wi = w.np_matrix_transform(numpy.linalg.inv, transpose_dims=True, row_space=hc) >>> wi == w.inv(hc) True
- nparray¶
nparray: numpy.ndarray
- op_norm(self, row_space=None, col_space=None)¶
Returns the maximum singular value of this operator.
Parameters: - row_space (HilbertSpace, list, or tuple) – the HilbertSpace to use for the row space of the matrix, default is the bra space of the input array.
- col_space (HilbertSpace, list, or tuple) – the HilbertSpace to use for the column space of the matrix, default is the ket space of the input array.
See also: schatten_norm()
>>> from qitensor import qudit >>> ha = qudit('a', 3) >>> sv = [2, 3, 7] >>> M = ha.random_unitary() * ha.diag(sv) * ha.random_unitary() >>> abs(M.op_norm() - 7) < 1e-14 True
- pinv(self, rcond=1e-15)¶
Returns the Moore-Penrose pseudoinverse of this array.
Parameters: rcond (float; default 1e-15) – cutoff for small singular values (see numpy.linalg.pinv docs for more info) >>> from qitensor import qubit, qudit >>> ha = qubit('a') >>> hb = qudit('b', 3) >>> x = (ha * hb.H).random_array() >>> x.as_np_matrix().shape (2, 3) >>> (x * x.pinv() - ha.eye()).norm() < 1e-13 True
- purity(self, normalize=False, checks=True)¶
Returns the purity of a density operator, (self*self).trace().
Parameters: - normalize (bool; default False) – if True, the input is automatically normalized to trace one. If false, an exception is raised if the trace is not one.
- checks (bool; default True) – if False, don’t check that the input is a valid density matrix or Hermitian. This is sometimes needed for symbolic computations.
>>> import numpy as np >>> from qitensor import qubit, qudit >>> ha = qubit('a') >>> # purity of a pure state is one >>> ha.ket(0).O.purity() 1.0 >>> # a fully mixed state of dimension 2 >>> (ha.ket(0).O/2 + ha.ket(1).O/2).purity() 0.5 >>> # automatic normalization >>> ha.eye().purity(normalize=True) 0.5
- relabel(self, from_spaces, to_spaces=None)¶
Returns a HilbertArray with the same data as this one, but with axes relabelled.
Parameters: - from_space (HilbertSpace, list, dict) – the old space, or list of spaces, or dict mapping old->new
- to_space (HilbertSpace, list) – the new space (or list of spaces)
This method changes the labels of the axes of this array. It is permitted to change a bra to a ket or vice-versa, in which case the effect is equivalent to doing a partial transpose. There are three ways to call this method:
- You can pass two HilbertSpaces, in which case the first space will be relabeled to the second one. If the passed spaces are not HilbertAtoms (i.e. they are composites like |a,b>) then the mapping from atom to atom is done using the same alphabetical sorting that is used when displaying the name of the space. In this case, the other two ways of calling relabel would probably be clearer.
- You can pass a pair of tuples of HilbertAtoms. In this case the first space from the first list gets renamed to the first space from the second list, and so on.
- You can pass a dictionary of HilbertAtoms of the form {from_atom => to_atom, ...}.
FIXME - does it return a view? should it?
>>> import numpy >>> from qitensor import qubit >>> ha = qubit('a') >>> hb = qubit('b') >>> hc = qubit('c') >>> x = (ha * hb).random_array() >>> x.space |a,b> >>> x.relabel(hb, hc).space |a,c> >>> numpy.allclose(x.relabel(hb, hc).nparray, x.nparray) True >>> x.relabel(ha, hc).space |b,c> >>> # underlying nparray is different because axes order changed >>> numpy.allclose(x.relabel(ha, hc).nparray, x.nparray) False >>> x.relabel(ha * hb, ha.prime * hb.prime).space |a',b'> >>> y = ha.O.array() >>> y.space |a><a| >>> # relabeling is needed because |a,a> is not allowed >>> y.relabel(ha.H, ha.prime.H).transpose(ha.prime).space |a,a'> >>> z = (ha*hb.H*hc.O).random_array() >>> z.space |a,c><b,c| >>> z1 = z.relabel((ha, hc.H), (ha.H, hc.prime)) >>> z1.space |c,c'><a,b| >>> z2 = z.relabel({ha: ha.H, hc.H: hc.prime}) >>> z2.space |c,c'><a,b| >>> z1 == z2 True >>> z == z1.relabel({ha.H: ha, hc.prime: hc.H}) True
- relabel_prime(self)¶
Returns a relabeled array with primed spaces.
See also: relabel(), qitensor.atom.HilbertAtom.prime()
>>> from qitensor import qubit >>> ha = qubit('a') >>> hb = qubit('b') >>> x = (ha*hb).array() >>> x.relabel_prime().space |a',b'> >>> (x * x.relabel_prime()).space |a,a',b,b'>
- relative_entropy(self, other, toler=1e-12)¶
FIXME - docs
>>> from qitensor import qudit >>> ha = qudit('a', 3) >>> hb = qudit('b', 4)
>>> rho = (ha*hb).random_density() >>> rho_a = rho.trace(hb) >>> rho_b = rho.trace(ha) >>> abs(rho.relative_entropy(rho_a * rho_b) - rho.mutual_info(ha, hb)) < 1e-14 True
>>> sigma = (ha*hb).random_density() >>> re1 = rho.relative_entropy(sigma) >>> re2 = (rho * (rho.logm() - sigma.logm())).trace() / np.log(2) >>> abs(re1 - re2) < 1e-13 True
>>> U = ha.random_unitary() >>> r = U * ha.diag([0.3, 0.7, 0]) * U.H >>> r.relative_entropy(r) < 1e-12 True >>> # A little fuzz is tolerated... >>> s = U * ha.diag([0.3, 0.7, 1e-13]) * U.H >>> s /= s.trace() >>> abs(s.relative_entropy(r)) < 1e-10 True >>> # ... but too much fuzz is not. >>> t = U * ha.diag([0.3, 0.7, 1e-6]) * U.H >>> t /= t.trace() >>> t.relative_entropy(r) inf
- sage_block_matrix(self, R=None)¶
Returns a Sage Matrix for this array, with blocks corresponding to subsystem structure.
sage: from qitensor import qubit sage: ha = qubit(‘a’, dtype=SR) sage: hb = qubit(‘b’, dtype=SR)
sage: (ha.X * hb.Z).sage_block_matrix() [ 0 0| 1 0] [ 0 0| 0 -1] [—–+—–] [ 1 0| 0 0] [ 0 -1| 0 0]
- sage_matrix(self, R=None)¶
Returns a Sage Matrix for this array.
It is probably preferable to just do Matrix(arr).
sage: from qitensor import qubit sage: ha = qubit(‘a’, dtype=SR) sage: v = ha.array([log(4), log(8)]) sage: v.sage_matrix() [log(4)] [log(8)]
- sage_matrix_transform(self, f, transpose_dims=False)¶
Just like np_matrix_transform() but does operations on a Sage Matrix.
sage: from qitensor import qubit sage: ha = qubit(‘a’, dtype=SR)
sage: ha.Y.sage_matrix_transform(lambda m: m.transpose()) HilbertArray(|a><a|, array([[0, I],
[-I, 0]], dtype=object))
- schatten_norm(self, p, row_space=None, col_space=None)¶
Returns the Schatten p-norm of this operator.
Parameters: - row_space (HilbertSpace, list, or tuple) – the HilbertSpace to use for the row space of the matrix, default is the bra space of the input array.
- col_space (HilbertSpace, list, or tuple) – the HilbertSpace to use for the column space of the matrix, default is the ket space of the input array.
See also: trace_norm()
>>> from qitensor import qubit, qudit >>> ha = qudit('a', 3) >>> sv = [2, 3, 7] >>> M = ha.random_unitary() * ha.diag(sv) * ha.random_unitary() >>> np.abs(M.schatten_norm(1) - np.sum([x for x in sv])) < 1e-14 True >>> np.abs(M.schatten_norm(4) - np.sum([x**4 for x in sv])**(1.0/4.0)) < 1e-14 True
- set_data(self, new_data)¶
Sets this array equal to the given argument.
Parameters: new_data (HilbertArray or anything that can be made into a numpy.array) – the new data >>> from qitensor import qubit >>> ha = qubit('a') >>> hb = qubit('b') >>> x = (ha*hb).array() >>> y = (ha*hb).random_array() >>> x.set_data(y) >>> x == y True >>> x.set_data([[1, 2], [3, 4]]) >>> x HilbertArray(|a,b>, array([[ 1.+0.j, 2.+0.j], [ 3.+0.j, 4.+0.j]]))
- simplify(self)¶
Simplifies symbolic expressions (only useful in Sage).
- simplify_full(self)¶
Simplifies symbolic expressions (only useful in Sage).
sage: from qitensor import qubit sage: ha = qubit(‘a’, dtype=SR) sage: v = ha.array([log(4), log(8)])
sage: v / log(2) HilbertArray(|a>, array([log(4)/log(2), log(8)/log(2)], dtype=object))
sage: (v / log(2)).simplify_full() HilbertArray(|a>, array([2, 3], dtype=object))
- singular_vals(self, row_space=None, col_space=None)¶
Returns the singular values of this array.
For the meaning of row_space and col_space, see the documentation for svd() or svd_list().
See also: svd(), svd_list()
>>> from qitensor import qubit, qudit >>> import numpy >>> ha = qubit('a') >>> hb = qubit('b') >>> hc = qubit('c') >>> x = (ha * hb.H * hc.H).random_array() >>> numpy.allclose(numpy.diag(x.svd()[1].as_np_matrix()), x.singular_vals()) True
- space¶
space: qitensor.space.HilbertSpace
- span(self, axes='all')¶
Returns a TensorSubspace for the column/row/mixed space of this array.
Parameters: axes – the axes to take the span of >>> from qitensor import qudit >>> ha = qudit('a', 2) >>> hb = qudit('b', 3) >>> hc = qudit('c', 3) >>> iso = (hb*ha.H).random_isometry() >>> proj = iso * iso.H >>> proj.span('col') <TensorSubspace of dim 2 over space (|b>)> >>> bigop = proj * ha.random_array() * hc.H.random_array() >>> bigop.space |a,b><b,c| >>> bigop.span('col') <TensorSubspace of dim 2 over space (|a,b>)> >>> bigop.span(hb.O) <TensorSubspace of dim 1 over space (|b><b|)>
- sqrt(self)¶
Return the square root of this matrix.
>>> from qitensor import qubit, qudit >>> ha = qubit('a') >>> hb = qudit('b', 3) >>> P = (ha*hb).O.random_array() >>> # make a positive operator >>> P = P.H * P >>> P.space |a,b><a,b| >>> Q = P.sqrt() >>> Q.space |a,b><a,b| >>> P.closeto(Q.H * Q) True >>> P.closeto(Q * Q.H) True
- svd(self, full_matrices=True, inner_space=None)¶
Return the singular value decomposition of this array.
Parameters: - full_matrices (bool; default True) – if True, U and V are square. If False, S is square.
- inner_space (HilbertSpace) – Hilbert space for S.
x.svd() returns a tuple (U, S, V) such that: * x == U * S * V * U.H * U is identity * S is diagonal * V * V.H is identity
If full_matrices is True:
- U and V will be square.
- If inner_space is None, the bra and ket spaces of U will be the same as the ket space of the input and the bra and ket spaces of V will be the same as the bra space of the input. The Hilbert space of S will be the same as that of the input. If the input is not square (the dimension of the bra space does not match that of the ket space) then S will not be square.
- If inner_space is not None, it should be a HilbertSpace whose bra and ket dimensions are the same as those of the input.
If full_matrices is False:
- S will be square. One of U or V will be square.
- If inner_space is None, the bra and ket spaces of S will be the same. Either the bra or the ket space of the input will be used for S, whichever is of smaller dimension. If they are of equal dimension but are not the same spaces, then there is an ambiguity and an exception will be raised. In this case, you must manually specify inner_space.
- If inner_space is not None, it should be a ket space, and must be of the same dimension as the smaller of the bra or ket spaces of the input. The given space will be used for both the bra and the ket space of S.
See also: singular_vals(), svd_list()
>>> from qitensor import qubit, qudit >>> ha = qubit('a') >>> hb = qubit('b') >>> hc = qubit('c') >>> x = (ha * hb.H * hc.H).random_array() >>> x.space |a><b,c|
>>> (U, S, V) = x.svd() >>> [h.space for h in (U, S, V)] [|a><a|, |a><b,c|, |b,c><b,c|] >>> (U * S * V - x).norm() < 1e-14 True
>>> (U, S, V) = x.svd(full_matrices=False) >>> [h.space for h in (U, S, V)] [|a><a|, |a><a|, |a><b,c|] >>> (U * S * V - x).norm() < 1e-14 True
>>> hS = qubit('d1') * qudit('d2', 4).H >>> hS |d1><d2| >>> (U, S, V) = x.svd(full_matrices=True, inner_space=hS) >>> [h.space for h in (U, S, V)] [|a><d1|, |d1><d2|, |d2><b,c|] >>> (U * S * V - x).norm() < 1e-14 True
>>> hS = qubit('d') >>> (U, S, V) = x.svd(full_matrices=False, inner_space=hS) >>> [h.space for h in (U, S, V)] [|a><d|, |d><d|, |d><b,c|] >>> (U * S * V - x).norm() < 1e-14 True
- svd_list(self, row_space=None, col_space=None, thresh=0)¶
Computes a singular value decomposition or Schmidt decomposition of this array.
x.svd_list() returns a tuple (U, S, V) such that:
- U is a list of arrays in the space defined by the row_space parameter (by default the bra space of the input)
- V is a list of arrays in the space defined by the col_space parameter (by default the ket space of the input)
- S is a 1-d numpy array of positive numbers (the singular values)
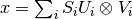
- The U are orthonormal, as are the V
Parameters: - row_space (HilbertSpace, list, or tuple) – the HilbertSpace to use for U, default is the bra space of the input array.
- col_space (HilbertSpace, list, or tuple) – the HilbertSpace to use for V, default is the ket space of the input array.
- thresh (float) – threshold below which singular values will be considered to be zero and discarded (default is to keep all singular values)
See also: singular_vals(), svd()
>>> from qitensor import qubit, qudit >>> ha = qudit('a', 3) >>> hb = qubit('b') >>> hc = qubit('c') >>> W = (ha * hb.H * hc.H).random_array() >>> W.space |a><b,c|
>>> # test basic properties of SVD >>> import numpy as np >>> (Ul, sl, Vl) = W.svd_list() >>> (len(Ul), len(sl), len(Vl)) (3, 3, 3) >>> (Ul[0].space, Vl[0].space) (|a>, <b,c|) >>> np.allclose(np.array([[x.H*y for x in Ul] for y in Ul]), np.eye(len(sl))) True >>> np.allclose(np.array([[x*y.H for x in Vl] for y in Vl]), np.eye(len(sl))) True >>> (np.sum([u*s*v for (u,s,v) in zip(Ul, sl, Vl)]) - W).norm() < 1e-14 True
>>> # take SVD across the |a><b| vs. <c| cut >>> import numpy >>> (Ul, sl, Vl) = W.svd_list(col_space=ha*hb.H) >>> (len(Ul), len(sl), len(Vl)) (2, 2, 2) >>> (Ul[0].space, Vl[0].space) (|a><b|, <c|) >>> np.allclose(np.array([[(x.H*y).trace() for x in Ul] for y in Ul]), np.eye(len(sl))) True >>> np.allclose(np.array([[x*y.H for x in Vl] for y in Vl]), np.eye(len(sl))) True >>> (np.sum([u*s*v for (u,s,v) in zip(Ul, sl, Vl)]) - W).norm() < 1e-14 True
>>> # as above, but with col_space given as a list >>> (Ul, sl, Vl) = W.svd_list(col_space=[hb.H, ha]) >>> (Ul[0].space, Vl[0].space) (|a><b|, <c|) >>> (np.sum([u*s*v for (u,s,v) in zip(Ul, sl, Vl)]) - W).norm() < 1e-14 True
- tensordot(self, HilbertArray other, contraction_spaces=None)¶
Inner or outer product of two arrays.
Parameters: - other (None, frozenset, or HilbertSpace; default None) – the other array taking place in this operation
- contraction_spaces – the spaces on which to do a tensor contraction
If contraction_spaces is None (the default), contraction will be across the intersection of the bra space of this array and the ket space of other. If a frozenset is given, it should consist of HilbertAtom objects which are kets. If a HilbertSpace is given, it must be a ket space.
>>> from qitensor import qubit >>> ha = qubit('a') >>> hb = qubit('b') >>> hc = qubit('c') >>> x = (ha * hb.H * hc.H).random_array() >>> x.space |a><b,c| >>> y = (hc * ha.H).random_array() >>> y.space |c><a| >>> x.tensordot(y) == x * y True >>> x.tensordot(y).space |a><a,b| >>> x.tensordot(y, frozenset()).space |a,c><a,b,c| >>> x.tensordot(y, hc).space |a><a,b| >>> (ha.bra(0) * hb.bra(0)) * (ha.ket(0) * hb.ket(0)) (1+0j) >>> (ha.bra(0) * hb.bra(0)) * (ha.ket(0) * hb.ket(1)) 0j >>> xa = ha.O.random_array() >>> xb = hb.O.random_array() >>> ((xa*xa)*(xb*xb)).space |a,b><a,b| >>> ((xa*xa)*(xb*xb)).closeto((xa*xb)*(xa*xb)) True
- trace(self, axes=None)¶
Returns the (full or partial) trace of this array.
FIXME - update docs with advanced trace features
Parameters: axes (HilbertSpace; default None) – axes to trace over, all axes if None (in which case the bra space must be the same as the ket space) >>> from qitensor import qubit, qudit >>> ha = qubit('a') >>> hb = qudit('b', 3) >>> hc = qubit('c') >>> x = ha.O.random_array() >>> y = hb.O.random_array() >>> z = hc.random_array() >>> abs(x.trace() - (x[0, 0] + x[1, 1])) < 1e-14 True >>> abs(y.trace() - (y[0, 0] + y[1, 1] + y[2, 2])) < 1e-14 True >>> abs(x.trace() * y.trace() - (x*y).trace()) < 1e-14 True >>> n = hb.random_array().normalized() >>> # trace of a projector >>> abs( (n*n.H).trace() - 1 ) < 1e-14 True >>> ( (x*y).trace(ha) - x.trace() * y ).norm() < 1e-14 True >>> ( (x*y).trace(hb) - x * y.trace() ).norm() < 1e-14 True >>> abs( (x*y).trace(ha*hb) - (x*y).trace() ) < 1e-14 True >>> abs( (x*y).trace(ha).trace(hb) - (x*y).trace() ) < 1e-14 True >>> abs( x.trace(ha) - x.trace(ha.H) ) < 1e-14 True >>> abs( x.trace(ha) - x.trace(ha.O) ) < 1e-14 True >>> ( (x*z).trace(ha) - x.trace() * z ).norm() < 1e-14 True >>> ( (x*z.H).trace(ha) - x.trace() * z.H ).norm() < 1e-14 True
>>> # trace between a pair of ket spaces (map-state duality stuff) >>> n = hb.random_array().normalized() >>> w = n.H.relabel({ hb.H: hb.prime }) * n * z >>> w.space |b,b',c> >>> w.trace({ hb: hb.prime }).space |c> >>> w.trace({ hb: hb.prime }).closeto(z) True >>> m = ha.random_array().normalized() >>> v = w * m * m.H.relabel(ha.H, hc.H) >>> v.space |a,b,b',c><c| >>> v.trace({ hb: hb.prime, hc.H: ha }).space |c> >>> v.trace({ hb: hb.prime, hc.H: ha }).closeto(z) True
- trace_norm(self, row_space=None, col_space=None)¶
Returns the sum of the singular values of this operator.
Parameters: - row_space (HilbertSpace, list, or tuple) – the HilbertSpace to use for the row space of the matrix, default is the bra space of the input array.
- col_space (HilbertSpace, list, or tuple) – the HilbertSpace to use for the column space of the matrix, default is the ket space of the input array.
See also: schatten_norm()
>>> from qitensor import qudit >>> ha = qudit('a', 3) >>> sv = [2, 3, 7] >>> M = ha.random_unitary() * ha.diag(sv) * ha.random_unitary() >>> abs(M.trace_norm() - 12) < 1e-14 True
- tracekeep(self, keep_spc)¶
Trace out all but the given spaces of a density operator. Actually, a density operator is not needed, but the bra and ket spaces must be the same.
FIXME - doctests
- transpose(self, tpose_axes=None)¶
Perform a transpose or partial transpose operation.
Parameters: tpose_axes (HilbertSpace or None; default None) – the space on which to transpose If tpose_axes is None a full transpose is performed. Otherwise, tpose_axes should be a HilbertSpace. The array will be transposed across all axes which are part of the bra space or ket space of tpose_axes.
>>> from qitensor import qubit >>> ha = qubit('a') >>> hb = qubit('b') >>> x = ha.O.array([[1, 2], [3, 4]]); x HilbertArray(|a><a|, array([[ 1.+0.j, 2.+0.j], [ 3.+0.j, 4.+0.j]])) >>> x.transpose() HilbertArray(|a><a|, array([[ 1.+0.j, 3.+0.j], [ 2.+0.j, 4.+0.j]])) >>> x.transpose() == x.T True >>> y = (ha * hb).random_array() >>> y.space |a,b> >>> y.transpose(ha).space |b><a| >>> y.transpose(ha) == y.transpose(ha.H) True