Hilbert Space Atoms

HilbertAtom repsenents the individible unit of HilbertSpace (i.e. qubits or qudits). At the same time, HilbertSpace is a base class for HilbertAtom. These are combined into larger product spaces by using the multiplication operator. HilbertAtoms should be created using the factory functions in qitensor.factory.

class qitensor.atom.HilbertAtom

Bases: qitensor.space.HilbertSpace

HilbertAtom(str label, str latex_label, tuple indices, group_op, base_field, dual)

X

HilbertAtom.X(self)

Returns the Pauli X operator.

This is only available for qubit spaces.

See also: pauliX()

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> ha.X
HilbertArray(|a><a|,
array([[ 0.+0.j,  1.+0.j],
       [ 1.+0.j,  0.+0.j]]))

Y

HilbertAtom.Y(self)

Returns the Pauli Y operator.

This is only available for qubit spaces.

See also: pauliY()

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> ha.Y
HilbertArray(|a><a|,
array([[ 0.+0.j, -0.-1.j],
       [ 0.+1.j,  0.+0.j]]))

Z

HilbertAtom.Z(self)

Returns the generalized Pauli Z operator.

See also: pauliZ()

>>> from qitensor import qubit, indexed_space

>>> ha = qubit('a')
>>> ha.Z
HilbertArray(|a><a|,
array([[ 1.+0.j,  0.+0.j],
       [ 0.+0.j, -1.+0.j]]))

>>> hb = indexed_space('b', ['x', 'y', 'z', 'w'])
>>> hb.Z
HilbertArray(|b><b|,
array([[ 1.+0.j,  0.+0.j,  0.+0.j,  0.+0.j],
       [ 0.+0.j,  0.+1.j,  0.+0.j,  0.+0.j],
       [ 0.+0.j,  0.+0.j, -1.+0.j,  0.+0.j],
       [ 0.+0.j,  0.+0.j,  0.+0.j, -0.-1.j]]))

bloch(self, theta, phi)

Returns a qubit state given its Bloch sphere representation (in radians).

>>> import numpy as np
>>> from qitensor import qubit
>>> ha = qubit('a')
>>> ha.bloch(0, 123) == ha.z_plus()
True
>>> ha.bloch(np.pi, 0).closeto(ha.z_minus())
True
>>> ha.bloch(np.pi/2, 0).closeto(ha.x_plus())
True
>>> ha.bloch(np.pi/2, np.pi/2).closeto(ha.y_plus())
True

bra(self, idx)

Returns a bra basis vector.

The returned vector has a 1 in the slot corresponding to idx and zeros elsewhere.

Parameters:idx – a member of this space’s index set

>>> from qitensor import qubit, indexed_space
>>> ha = qubit('a')
>>> hb = indexed_space('b', ['x', 'y', 'z'])

>>> ha.bra(0)
HilbertArray(<a|,
array([ 1.+0.j,  0.+0.j]))

>>> hb.bra('y')
HilbertArray(<b|,
array([ 0.+0.j,  1.+0.j,  0.+0.j]))

static direct_sum(type cls, kets)

Returns the direct sum of this atom with another, along with a pair of isometries mapping to the sum space.

>>> from qitensor import qudit, direct_sum
>>> ha = qudit('a', 2)
>>> hb = qudit('b', 3)
>>> hab = direct_sum((ha, hb))
>>> (hab, hab.P[0].space, hab.P[1].space)
(|a+b>, |a+b><a|, |a+b><b|)
>>> x = ha.random_array()
>>> y = hb.random_array()
>>> z = hab.P[0]*x + hab.P[1]*y
>>> x == hab.P[0].H * z
True
>>> y == hab.P[1].H * z
True

>>> # it is allowed to repeat a space
>>> haa = direct_sum((ha, ha))
>>> (haa, haa.P[0].space, haa.P[1].space)
(|a+a>, |a+a><a|, |a+a><a|)
>>> x1 = ha.random_array()
>>> x2 = ha.random_array()
>>> z = haa.P[0]*x1 + haa.P[1]*x2
>>> x1 == haa.P[0].H * z
True
>>> x2 == haa.P[1].H * z
True

gateS(self)

Returns the S-gate operator.

This is only available for qubit spaces.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> ha.gateS()
HilbertArray(|a><a|,
array([[ 1.+0.j,  0.+0.j],
       [ 0.+0.j,  0.+1.j]]))

gateT(self)

Returns the T-gate operator.

This is only available for qubit spaces.

>>> from qitensor import qubit

>>> ha = qubit('a')
>>> ha.gateT()
HilbertArray(|a><a|,
array([[ 1.000000+0.j      ,  0.000000+0.j      ],
       [ 0.000000+0.j      ,  0.707107+0.707107j]]))

group_op

group_op: object

indices

indices: tuple

is_dual

is_dual: __builtin__.bool

ket(self, idx)

Returns a ket basis vector.

The returned vector has a 1 in the slot corresponding to idx and zeros elsewhere.

Parameters:idx – a member of this space’s index set

>>> from qitensor import qubit, indexed_space
>>> ha = qubit('a')
>>> hb = indexed_space('b', ['x', 'y', 'z'])

>>> ha.ket(0)
HilbertArray(|a>,
array([ 1.+0.j,  0.+0.j]))

>>> hb.ket('y')
HilbertArray(|b>,
array([ 0.+0.j,  1.+0.j,  0.+0.j]))

key

key: tuple

label

label: str

latex_label

latex_label: str

pauliX(self, h=None, left=True)

Returns the Pauli X operator.

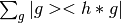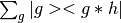If h is given, then the group Pauli X operator is returned. If left is True, the return value is . If left is False, the return value is . For qudit spaces, the default group operation is modular addition. For indexed_space spaces the default operation is multiplication, and an error is thrown if the index set is not closed under this operation.

If h is not given, the default of 1 is used for cyclic addition groups (the default group), otherwise an error is thrown.

NOTE: some people use a convention that is a transpose of this!

See also: X()

>>> import numpy as np
>>> from qitensor import qubit, qudit, indexed_space, dihedral_group

>>> ha = qubit('a')
>>> ha.pauliX()
HilbertArray(|a><a|,
array([[ 0.+0.j,  1.+0.j],
       [ 1.+0.j,  0.+0.j]]))

>>> hb = qudit('b', 3)
>>> hb.pauliX()
HilbertArray(|b><b|,
array([[ 0.+0.j,  1.+0.j,  0.+0.j],
       [ 0.+0.j,  0.+0.j,  1.+0.j],
       [ 1.+0.j,  0.+0.j,  0.+0.j]]))

>>> hb.pauliX(2)
HilbertArray(|b><b|,
array([[ 0.+0.j,  0.+0.j,  1.+0.j],
       [ 1.+0.j,  0.+0.j,  0.+0.j],
       [ 0.+0.j,  1.+0.j,  0.+0.j]]))

>>> S3 = dihedral_group(3)
>>> hc = indexed_space('c', S3.elements)
>>> np.all([hc.pauliX(f) * hc.ket(f*g) == hc.ket(g) for f in S3.elements for g in S3.elements])
True
>>> np.all([hc.pauliX(f, left=False) * hc.ket(g*f) == hc.ket(g) for f in S3.elements for g in S3.elements])
True

pauliY(self)

Returns the Pauli Y operator.

This is only available for qubit spaces.

See also: Y()

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> ha.pauliY()
HilbertArray(|a><a|,
array([[ 0.+0.j, -0.-1.j],
       [ 0.+1.j,  0.+0.j]]))

pauliZ(self, int order=1)

Returns the generalized Pauli Z operator.

Parameters:order (integer; default 1) – if given, 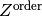will be returned. This is only useful for spaces that are larger than qubits.

The return value is .

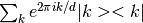See also: Z()

>>> from qitensor import qubit, indexed_space

>>> ha = qubit('a')
>>> ha.pauliZ()
HilbertArray(|a><a|,
array([[ 1.+0.j,  0.+0.j],
       [ 0.+0.j, -1.+0.j]]))

>>> hb = indexed_space('b', ['x', 'y', 'z', 'w'])
>>> hb.pauliZ()
HilbertArray(|b><b|,
array([[ 1.+0.j,  0.+0.j,  0.+0.j,  0.+0.j],
       [ 0.+0.j,  0.+1.j,  0.+0.j,  0.+0.j],
       [ 0.+0.j,  0.+0.j, -1.+0.j,  0.+0.j],
       [ 0.+0.j,  0.+0.j,  0.+0.j, -0.-1.j]]))

>>> hb.pauliZ(2)
HilbertArray(|b><b|,
array([[ 1.+0.j,  0.+0.j,  0.+0.j,  0.+0.j],
       [ 0.+0.j, -1.+0.j,  0.+0.j,  0.+0.j],
       [ 0.+0.j,  0.+0.j,  1.-0.j,  0.+0.j],
       [ 0.+0.j,  0.+0.j,  0.+0.j, -1.+0.j]]))

prime

HilbertAtom.prime(self)

Returns a HilbertAtom just like this one but with an apostrophe appended to the label.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> ha.prime
|a'>
>>> ha.prime.prime
|a''>

x_minus(self)

Returns the state [1, -1]/sqrt(2), only available for qubits.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> '%g' % ha.x_minus().norm()
'1'
>>> ha.X * ha.x_minus() == -ha.x_minus()
True

x_plus(self)

Returns a state with 1/sqrt(D) in each slot.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> '%g' % ha.x_plus().norm()
'1'
>>> ha.X * ha.x_plus() == ha.x_plus()
True

y_minus(self)

Returns the state [1, I]/sqrt(2), only available for qubits.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> '%g' % ha.y_minus().norm()
'1'
>>> ha.Y * ha.y_minus() == -ha.y_minus()
True

y_plus(self)

Returns the state [1, I]/sqrt(2), only available for qubits.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> '%g' % ha.y_plus().norm()
'1'
>>> ha.Y * ha.y_plus() == ha.y_plus()
True

z_minus(self)

Returns the state [0, 1], only available for qubits.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> '%g' % ha.z_minus().norm()
'1'
>>> ha.Z * ha.z_minus() == -ha.z_minus()
True

z_plus(self)

Returns the state [1, 0], only available for qubits.

>>> from qitensor import qubit
>>> ha = qubit('a')
>>> '%g' % ha.z_plus().norm()
'1'
>>> ha.Z * ha.z_plus() == ha.z_plus()
True

qitensor.atom.direct_sum(type cls, kets)

Returns the direct sum of this atom with another, along with a pair of isometries mapping to the sum space.

>>> from qitensor import qudit, direct_sum
>>> ha = qudit('a', 2)
>>> hb = qudit('b', 3)
>>> hab = direct_sum((ha, hb))
>>> (hab, hab.P[0].space, hab.P[1].space)
(|a+b>, |a+b><a|, |a+b><b|)
>>> x = ha.random_array()
>>> y = hb.random_array()
>>> z = hab.P[0]*x + hab.P[1]*y
>>> x == hab.P[0].H * z
True
>>> y == hab.P[1].H * z
True

>>> # it is allowed to repeat a space
>>> haa = direct_sum((ha, ha))
>>> (haa, haa.P[0].space, haa.P[1].space)
(|a+a>, |a+a><a|, |a+a><a|)
>>> x1 = ha.random_array()
>>> x2 = ha.random_array()
>>> z = haa.P[0]*x1 + haa.P[1]*x2
>>> x1 == haa.P[0].H * z
True
>>> x2 == haa.P[1].H * z
True