Circuit Functions¶

This module contains functions related to quantum circuits.

qitensor.circuit.cphase(h1, h2)¶

Returns the controlled-phase or generalized controlled-phase gate.

The given spaces must be HilbertAtom spaces (i.e. not tensor products).

For qubits, returns an operator in h1*h2 given by the diagonal array [1, 1, 1, -1].

For larger dimension spaces, h1 and h2 must be of the same dimension (call it D) and the operator returned is given by 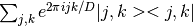$\sum_{j,k} e^{2 \pi i j k / D} |j,k><j,k|$ , where j and k are taken to be integer indices, regardless of the actual contents of the space’s index set.

>>> from qitensor import qubit, cphase

>>> ha = qubit('a')
>>> hb = qubit('b')
>>> cphase(ha, hb).as_np_matrix()
matrix([[ 1.+0.j,  0.+0.j,  0.+0.j,  0.+0.j],
        [ 0.+0.j,  1.+0.j,  0.+0.j,  0.+0.j],
        [ 0.+0.j,  0.+0.j,  1.+0.j,  0.+0.j],
        [ 0.+0.j,  0.+0.j,  0.+0.j, -1.+0.j]])

>>> U = cphase(ha*ha.prime, hb*hb.prime)
>>> V01 = ha.bra(0) * ha.prime.bra(1) * U * ha.ket(0) * ha.prime.ket(1)
>>> (V01 - (hb*hb.prime).diag([1, 1j, -1, -1j])).norm() < 1e-14
True
>>> V10 = ha.bra(1) * ha.prime.bra(0) * U * ha.ket(1) * ha.prime.ket(0)
>>> (V10 - (hb*hb.prime).diag([1, -1, 1, -1])).norm() < 1e-14
True

>>> cphase(ha*ha.prime, hb)
Traceback (most recent call last):
    ...
HilbertError: 'spaces must be of the same dimension'

>>> cphase(ha.H, hb)
Traceback (most recent call last):
    ...
NotKetSpaceError: '<a|'

qitensor.circuit.cnot(h1, h2, left=True)¶

Returns the controlled-not (controlled-X) gate.

The given spaces must be HilbertAtom spaces (i.e. not tensor products). FIXME - need docs for non-qubit case FIXME - doctest for group_op

>>> from qitensor import qubit, qudit, indexed_space, dihedral_group, cnot
>>> ha = qubit('a')
>>> hb = qubit('b')
>>> cnot(ha, hb).as_np_matrix()
matrix([[ 1.+0.j,  0.+0.j,  0.+0.j,  0.+0.j],
        [ 0.+0.j,  1.+0.j,  0.+0.j,  0.+0.j],
        [ 0.+0.j,  0.+0.j,  0.+0.j,  1.+0.j],
        [ 0.+0.j,  0.+0.j,  1.+0.j,  0.+0.j]])
>>> cnot(hb, ha).as_np_matrix()
matrix([[ 1.+0.j,  0.+0.j,  0.+0.j,  0.+0.j],
        [ 0.+0.j,  0.+0.j,  0.+0.j,  1.+0.j],
        [ 0.+0.j,  0.+0.j,  1.+0.j,  0.+0.j],
        [ 0.+0.j,  1.+0.j,  0.+0.j,  0.+0.j]])

>>> hc = qudit('a', 3)
>>> hc.bra(1) * cnot(hc, hc.prime) * hc.ket(1)
HilbertArray(|a'><a'|,
array([[ 0.+0.j,  1.+0.j,  0.+0.j],
       [ 0.+0.j,  0.+0.j,  1.+0.j],
       [ 1.+0.j,  0.+0.j,  0.+0.j]]))

>>> S3 = dihedral_group(3)
>>> hd = indexed_space('d', S3.elements)
>>> hd.bra(S3.r1) * cnot(hd, hd.prime) * hd.ket(S3.r1) == hd.prime.pauliX(S3.r1)
True
>>> hd.bra(S3.r1) * cnot(hd, hd.prime, left=False) * hd.ket(S3.r1) == hd.prime.pauliX(S3.r1, left=False)
True

qitensor.circuit.swap(h1, h2)¶

Returns the swap gate.

The given spaces must be of the same dimension.

>>> from qitensor import qubit, qudit, swap
>>> ha = qubit('a')
>>> hb = qudit('b', 4)
>>> hc = qubit('c')
>>> swap(ha, hc).as_np_matrix()
matrix([[ 1.+0.j,  0.+0.j,  0.+0.j,  0.+0.j],
        [ 0.+0.j,  0.+0.j,  1.+0.j,  0.+0.j],
        [ 0.+0.j,  1.+0.j,  0.+0.j,  0.+0.j],
        [ 0.+0.j,  0.+0.j,  0.+0.j,  1.+0.j]])
>>> swap(ha, hb).as_np_matrix()
Traceback (most recent call last):
    ...
HilbertShapeError: '2 vs. 4'
>>> psi = (ha*hc).random_array()
>>> phi = hb.random_array()
>>> psi2 = hb.array(psi.nparray, reshape=True)
>>> phi2 = (ha*hc).array(phi.nparray, reshape=True)
>>> (psi2*phi2 - swap(ha*hc, hb)*psi*phi).norm() < 1e-14
True

qitensor.circuit.controlled_U(cspc, U)¶

FIXME - docs

>>> from qitensor import qubit, qudit, controlled_U, cnot, swap
>>> ha = qubit('a')
>>> hb = qubit('b')
>>> hc = qubit('c')
>>> hd = qudit('d', 3)

>>> controlled_U(ha, hb.X) == cnot(ha, hb)
True
>>> controlled_U(ha, [hb.Z, hb.Z * hb.X]) == hb.Z * cnot(ha, hb)
True

>>> U = controlled_U(hd, [ha.X, ha.Y, ha.Z])
>>> U == controlled_U(hd, {0: ha.X, 1: ha.Y, 2: ha.Z})
True
>>> U * hd.ket(0) == ha.X * hd.ket(0)
True
>>> U * hd.ket(1) == ha.Y * hd.ket(1)
True
>>> U * hd.ket(2) == ha.Z * hd.ket(2)
True

>>> V = controlled_U(ha, cnot(hb, hc))
>>> V == controlled_U(ha*hb, {(1,1): hc.X})
True
>>> V * ha.ket(0) == (hb*hc).eye() * ha.ket(0)
True
>>> V * ha.ket(1) == cnot(hb, hc) * ha.ket(1)
True

qitensor.circuit.toffoli(ha, hb, hc)¶

FIXME - docs

>>> from qitensor import qubit, toffoli
>>> ha = qubit('a')
>>> hb = qubit('b')
>>> hc = qubit('c')
>>> U = toffoli(ha, hb, hc)
>>> U * ha.ket(0) == (hb*hc).eye() * ha.ket(0)
True
>>> U * ha.ket(1) == cnot(hb, hc) * ha.ket(1)
True

qitensor.circuit.fredkin(ha, hb, hc)¶

FIXME - docs

>>> from qitensor import qubit, fredkin
>>> ha = qubit('a')
>>> hb = qubit('b')
>>> hc = qubit('c')
>>> U = fredkin(ha, hb, hc)
>>> U * ha.ket(0) == (hb*hc).eye() * ha.ket(0)
True
>>> U * ha.ket(1) == swap(hb, hc) * ha.ket(1)
True

qitensor.circuit.max_entangled(h1, h2)¶

Returns a maximally entangled state.

The given spaces must be HilbertAtom spaces (i.e. not tensor products). The spaces must also be of equal dimension (call it D). The returned state is 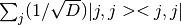$\sum_j (1/\sqrt{D}) |j,j><j,j|$ , where j is taken to be an integer index, regardless of the actual contents of the space’s index set.

>>> from qitensor import qubit, qudit, indexed_space, max_entangled

>>> ha = qubit('a')
>>> hb = qubit('b')
>>> max_entangled(ha, hb)
HilbertArray(|a,b>,
array([[ 0.707107+0.j,  0.000000+0.j],
       [ 0.000000+0.j,  0.707107+0.j]]))

>>> ha = qudit('a', 4)
>>> hb = qudit('b', 4)
>>> max_entangled(ha, hb)
HilbertArray(|a,b>,
array([[ 0.5+0.j,  0.0+0.j,  0.0+0.j,  0.0+0.j],
       [ 0.0+0.j,  0.5+0.j,  0.0+0.j,  0.0+0.j],
       [ 0.0+0.j,  0.0+0.j,  0.5+0.j,  0.0+0.j],
       [ 0.0+0.j,  0.0+0.j,  0.0+0.j,  0.5+0.j]]))

>>> ha = qudit('a', 4)
>>> hb = indexed_space('b', ['w', 'x', 'y', 'z'])
>>> max_entangled(ha, hb)
HilbertArray(|a,b>,
array([[ 0.5+0.j,  0.0+0.j,  0.0+0.j,  0.0+0.j],
       [ 0.0+0.j,  0.5+0.j,  0.0+0.j,  0.0+0.j],
       [ 0.0+0.j,  0.0+0.j,  0.5+0.j,  0.0+0.j],
       [ 0.0+0.j,  0.0+0.j,  0.0+0.j,  0.5+0.j]]))

>>> psi1 = max_entangled(ha, ha.prime) * max_entangled(hb, hb.prime)
>>> psi2 = max_entangled(ha*hb, (ha*hb).prime)
>>> (psi1 - psi2).norm() < 1e-14
True

>>> max_entangled(ha*ha.prime, hb)
Traceback (most recent call last):
    ...
HilbertError: 'spaces must be of the same dimension'

>>> max_entangled(ha.H, hb)
Traceback (most recent call last):
    ...
NotKetSpaceError: '<a|'

Circuit Functions¶

Previous topic

Next topic

This Page

Navigation

Circuit Functions¶

Previous topic

Next topic

This Page

Quick search

Navigation