Tensor Subspaces¶

class qitensor.subspace.TensorSubspace(basis, perp_basis, tol, hilb_space, validate=False)¶

Bases: object

Represents a basis of a tensor subspace. Methods are available for projecting to this basis, computing span and intersection of subspaces, etc. This module can be used independently of qitensor, and the doctest below reflects this. However, if you are using qitensor then typically a subspace would be created using one of the following methods:

>>> import numpy as np
>>> from qitensor import TensorSubspace
>>> x = TensorSubspace.from_span(np.random.randn(4,5,10))
>>> x
<TensorSubspace of dim 4 over space (5, 10)>
>>> x.dim()
4
>>> x[0] in x
True
>>> x.perp()[0] in x
False
>>> y = TensorSubspace.from_span(np.random.randn(30,5,10))
>>> y
<TensorSubspace of dim 30 over space (5, 10)>
>>> z = TensorSubspace.from_span(np.random.randn(30,5,10))
>>> z
<TensorSubspace of dim 30 over space (5, 10)>
>>> x | y
<TensorSubspace of dim 34 over space (5, 10)>
>>> y | z
<TensorSubspace of dim 50 over space (5, 10)>
>>> y & z
<TensorSubspace of dim 10 over space (5, 10)>
>>> y > x&y
True
>>> y > x|y
False
>>> x|y > y
True
>>> y - x
<TensorSubspace of dim 26 over space (5, 10)>
>>> (y & z).equiv(~(~y | ~z))
True
>>> (y-(y-x)).equiv(TensorSubspace.from_span([ y.project(v) for v in x ]))
True

assert_compatible(other)¶

Raise error if other is not compatible with this space. Compatible means that the dimensions are the same and that the HilbertSpaces match if both subspaces have that property.

>>> from qitensor import TensorSubspace
>>> spc1 = TensorSubspace.full((3,5))
>>> spc2 = TensorSubspace.empty((3,5))
>>> spc3 = TensorSubspace.empty((3,6))
>>> spc1.assert_compatible(spc2)
>>> spc1.assert_compatible(spc3)
Traceback (most recent call last):
    ...
AssertionError

contains(other)¶

Tests whether the given TensorSubspace or vector is contained in this space. Equivalent to self > other.

>>> import numpy as np
>>> from qitensor import TensorSubspace
>>> x = TensorSubspace.from_span(np.random.randn(4,5,10))
>>> y = TensorSubspace.from_span(np.random.randn(30,5,10))
>>> y.contains(x)
False
>>> (y|x).contains(x)
True
>>> x.contains(y[0])
False
>>> y.contains(y[0])
True

dim()¶

Returns the dimension of this subspace.

>>> import numpy as np
>>> from qitensor import TensorSubspace
>>> x = TensorSubspace.from_span(np.random.randn(4,10,10))
>>> x.dim()
4

classmethod empty(col_shp, tol=1e-10, hilb_space=None, dtype=<type 'complex'>)¶

Constructs the empty subspace of the given dimension.

>>> from qitensor import TensorSubspace
>>> TensorSubspace.empty((3,5))
<TensorSubspace of dim 0 over space (3, 5)>

equiv(other)¶

Tests whether this subspace is equal to other, to within an error tolerance. Equivalent to self < other and self > other.

>>> import numpy as np
>>> from qitensor import TensorSubspace
>>> x = TensorSubspace.from_span(np.random.randn(4,5,10))
>>> y = TensorSubspace.from_span(np.random.randn(30,5,10))
>>> x.equiv(y)
False
>>> (x & y).equiv(~(~x | ~y))
True

from_basis(v)¶

Returns the element of this subspace corresponding to the given vector, which is to be expressed in this subspace’s basis.

>>> import numpy as np
>>> from qitensor import TensorSubspace
>>> spc = TensorSubspace.from_span(np.random.randn(4,5,10))
>>> spc
<TensorSubspace of dim 4 over space (5, 10)>
>>> spc.dim()
4
>>> np.allclose(spc[0], spc.from_basis([1,0,0,0]))
True
>>> np.allclose(spc[1], spc.from_basis([0,1,0,0]))
True
>>> v = np.random.randn(5,10)
>>> w = spc.from_basis(spc.to_basis(v))
>>> np.allclose(w, spc.project(v))
True

classmethod from_span(X, tol=1e-10, hilb_space=None, dtype=None)¶

Construct a TensorSubspace that represents the span of the given operators.

Parameters:	X (list of numpy array or numpy array whose first axes indexes the operators) – the operators to take the span of. tol – tolerance for determining whether operators are perpendicular dtype – the datatype (default is to use the datatype of the input operators)

>>> from qitensor import TensorSubspace
>>> import numpy as np
>>> x = np.random.randn(3, 5)
>>> y = np.random.randn(3, 5)
>>> TensorSubspace.from_span([x, y])
<TensorSubspace of dim 2 over space (3, 5)>
>>> TensorSubspace.from_span([x, y, 2*x+0.3*y])
<TensorSubspace of dim 2 over space (3, 5)>
>>> TensorSubspace.from_span(x)
<TensorSubspace of dim 3 over space (5,)>

classmethod full(col_shp, tol=1e-10, hilb_space=None, dtype=<type 'complex'>)¶

Constructs the full subspace of the given dimension.

>>> from qitensor import TensorSubspace
>>> TensorSubspace.full((3,5))
<TensorSubspace of dim 15 over space (3, 5)>

hermitian_basis()¶

Compute a basis for the Hermitian operators of this space. Note that this basis is intended to map real vectors to complex operators.

>>> import numpy as np
>>> from qitensor import TensorSubspace
>>> S = TensorSubspace.from_span(np.random.randn(4,10,10))
>>> S.hermitian_basis() # S is not Hermitian
Traceback (most recent call last):
    ...
AssertionError
>>> T = S | TensorSubspace.from_span([ x.transpose().conjugate() for x in S ])
>>> hbas = T.hermitian_basis()
>>> hbas.shape[0] == T.dim()
True
>>> x = np.tensordot(np.random.randn(hbas.shape[0]), hbas, axes=([0],[0]))
>>> np.allclose(x, x.transpose().conjugate())
True
>>> x in T
True

is_hermitian()¶

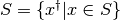A subspace S is Hermitian if $S = \{ x^\dagger | x \in S \}$ .

>>> import numpy as np
>>> from qitensor import TensorSubspace
>>> S = TensorSubspace.from_span(np.random.randn(4,10,10))
>>> S.is_hermitian()
False
>>> T = S | TensorSubspace.from_span([ x.transpose().conjugate() for x in S ])
>>> T.is_hermitian()
True

is_perp(other)¶

Tests whether the given TensorSubspace or vector is perpendicular to this space.

>>> import numpy as np
>>> from qitensor import TensorSubspace
>>> x = TensorSubspace.from_span(np.random.randn(4,5,10))
>>> y = TensorSubspace.from_span(np.random.randn(30,5,10))
>>> x.is_perp(y)
False
>>> x.is_perp(~x)
True
>>> x.is_perp(y-x)
True
>>> y.is_perp(x[0])
False
>>> (y-x).is_perp(x[0])
True

map(f)¶

perp()¶

Returns orthogonal complement of this space. Equivalent to ~self.

>>> from qitensor import TensorSubspace
>>> import numpy as np
>>> x = np.random.randn(3, 5)
>>> y = np.random.randn(3, 5)
>>> spc = TensorSubspace.from_span([x, y]); spc
<TensorSubspace of dim 2 over space (3, 5)>
>>> spc.perp()
<TensorSubspace of dim 13 over space (3, 5)>
>>> spc.equiv(spc.perp().perp())
True
>>> TensorSubspace.full((3,5)).perp().equiv(TensorSubspace.empty((3,5)))
True
>>> TensorSubspace.empty((3,5)).perp().equiv(TensorSubspace.full((3,5)))
True

project(x)¶

Returns the element of this subspace that is the closest to the given tensor.

>>> import numpy as np
>>> from qitensor import TensorSubspace
>>> spc = TensorSubspace.from_span(np.random.randn(4,5,10))
>>> v = np.random.randn(5,10)
>>> np.allclose(spc[0], spc.project(spc[0]))
True
>>> np.allclose(v, spc.project(v))
False
>>> w = spc.from_basis(spc.to_basis(v))
>>> np.allclose(w, spc.project(v))
True

random_hermit()¶

Returns a random Hermitian vector in this subspace.

>>> import numpy as np
>>> from qitensor import TensorSubspace
>>> S = TensorSubspace.from_span(np.random.randn(4,10,10))
>>> S.random_hermit() # S is not Hermitian
Traceback (most recent call last):
    ...
AssertionError
>>> T = S | TensorSubspace.from_span([ x.transpose().conjugate() for x in S ])
>>> v = T.random_hermit()
>>> np.allclose(v, v.transpose().conjugate())
True
>>> v in T
True

random_vec()¶

Returns a random vector in this subspace.

>>> import numpy as np
>>> from qitensor import TensorSubspace
>>> x = TensorSubspace.from_span(np.random.randn(4,5,10))
>>> x
<TensorSubspace of dim 4 over space (5, 10)>
>>> v = x.random_vec()
>>> v in x
True
>>> abs(1 - np.linalg.norm(v)) < 1e-13
True
>>> x.equiv(TensorSubspace.from_span([ x.random_vec() for i in range(x.dim()) ]))
True

reshape(shape)¶

tensor_prod(other)¶

to_basis(x)¶

Returns a representation of tensor x as a vector in the basis of this subspace. If x is not in this subspace, the orthogonal projection is used (i.e. the element of the subspace closest to x).

>>> import numpy as np
>>> from qitensor import TensorSubspace
>>> spc = TensorSubspace.from_span(np.random.randn(4,5,10))
>>> spc
<TensorSubspace of dim 4 over space (5, 10)>
>>> spc.dim()
4
>>> np.allclose(spc.to_basis(spc[0]), np.array([1,0,0,0]))
True
>>> np.allclose(spc.to_basis(spc[1]), np.array([0,1,0,0]))
True
>>> v = np.random.randn(5,10)
>>> spc.to_basis(v).shape
(4,)
>>> w = spc.from_basis(spc.to_basis(v))
>>> np.allclose(w, spc.project(v))
True

transpose(axes)¶

Tensor Subspaces¶

Previous topic

Next topic

This Page

Navigation

Tensor Subspaces¶

Previous topic

Next topic

This Page

Quick search

Navigation